函数
函数又被叫做子程序,有一或多个语句项组成,负责完成某项特定任务。通常我们是将一项任务或者功能封装在一个函数中,对外提供接口,这样代码更加结构化。
特点:
- 具备相对的独立性
- 一般有输入值和返回值
- 功能单一且灵活
1. 库函数
1.1 库函数的定义
库函数,就是放在库里供他人使用的函数。
如打印输出这样的基础功能,他不是业务性的代码,在开发过程中使用率高且可移植性强,故C语言的基础库里提供了这样的一系列基础功能的代码。
一般库函数有:
- IO函数(input&output)—— printf scanf getchar putchar …
- 字符串操作函数 —— strlen strcmp strcat strcpy …
- 字符操作函数 —— tolower toupper …
- 内存操作函数 —— memcpy menset memmove memcmp …
- 时间/日期操作函数 —— time …
- 数学函数 —— sqrt abs fabs pow …
- 其他库函数
1.2 介绍
查看库函数可以以 c/cpp权威网站 cplusplus 的解析为样本,不同平台也是大同小异。
- 函数的基本信息:函数名,参数,返回类型
- 功能描述:函数的具体作用
strcpy
char* strcpy (char* destination, const char* source);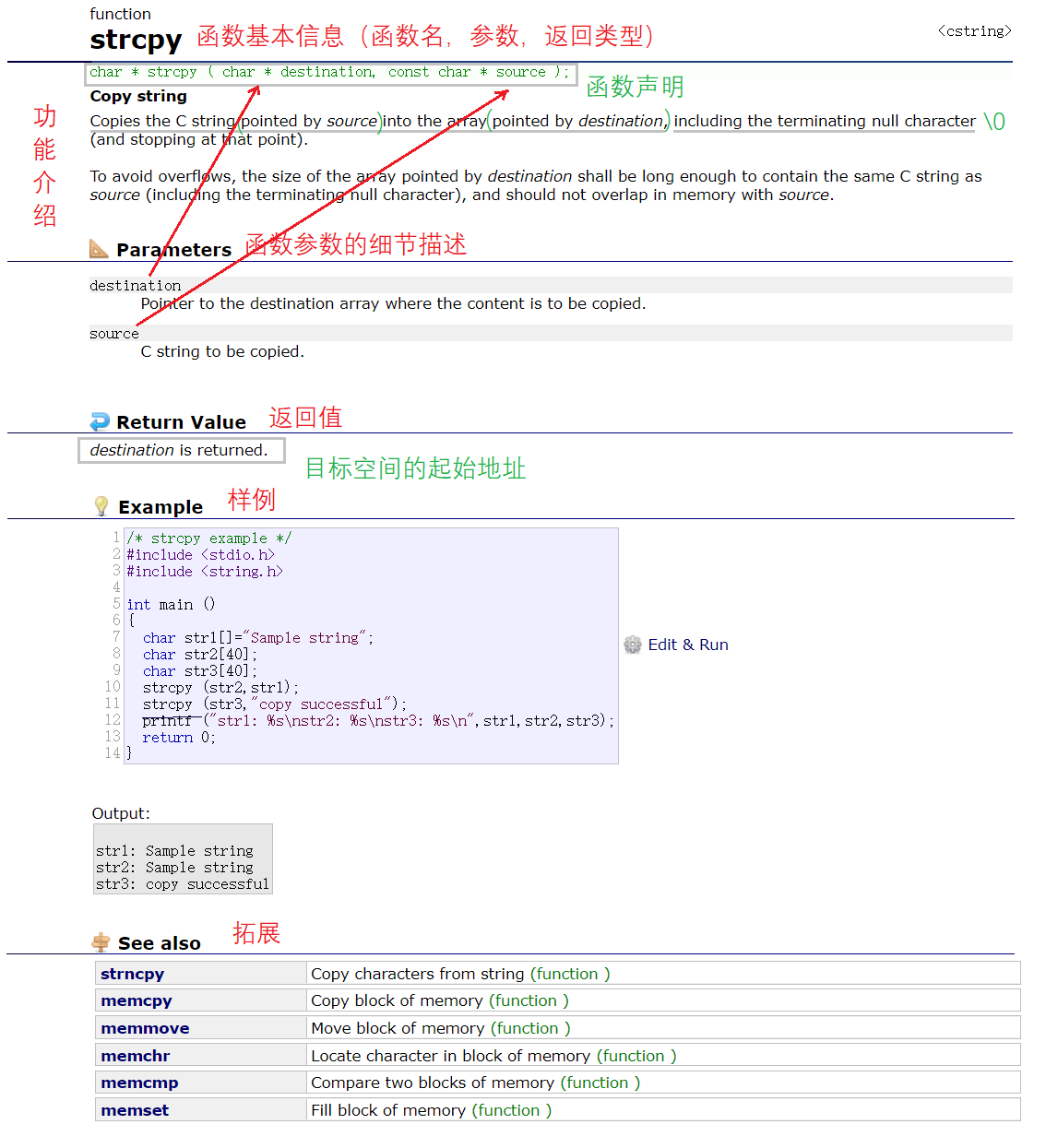
//当然这里 strcpy 函数的返回值是目标空间的首地址,故接收时也可以使用函数的返回值。
char arr1[20] = { 0 };
char arr2[] = "damn it!";
//1.
char* ret = strcpy(arr1, arr2);
printf("%s\n", ret);
//2.
printf("%s\n",strcpy(arr1, arr2));memset
void* (void* ptr, int value, size_t num);memset 是以字节为单位,修改地址中的内容。
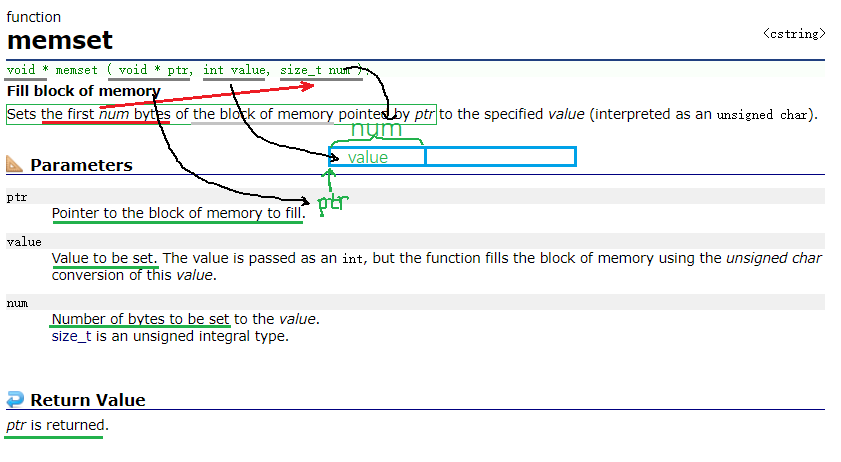
int arr[30];
memset(arr, 0, 30 * sizeof(int));
2. 自定义函数
2.1 自定义函数的定义
库函数虽多,但毕竟是有限的,还是需要自定义函数来实现某些具体的需求。自定义函数和库函数一样,有函数名、返回类型和函数参数,但不同的是这些都由我们自己来设计。
ret_type fun_name (para1, ...)
{
statment;//语句项
}
ret_type //返回类型
fun_name //函数名
para1 //参数找最大值

如图所示,写函数,函数名、参数、返回类型都要对应。
2.2 函数的参数
函数参数分为实际参数和形式参数两种:
- 实际参数又叫实参,实参可以是任意有确定值的形式,以便在进行函数调用时,将其传给形参。
- 形式参数又叫形参,只有当函数调用时,他们才被分配确定值以及内存单元,调前不存在,调后销毁,所以形参只是形式上存在。
2.3 函数的调用
- 传值调用
形参相当于实参的一份临时拷贝,并且形参和实参占用不同的内存单元,本质上是两个不同的变量,形参的修改不影响实参。
- 传址调用
将外部变量的地址传给函数参数,这样的调用可使函数内外建立真正的联系,即形参实参建立联系。
两数交换
先看在程序设计中如何进行两数交换,用酱油、醋和空瓶举例。
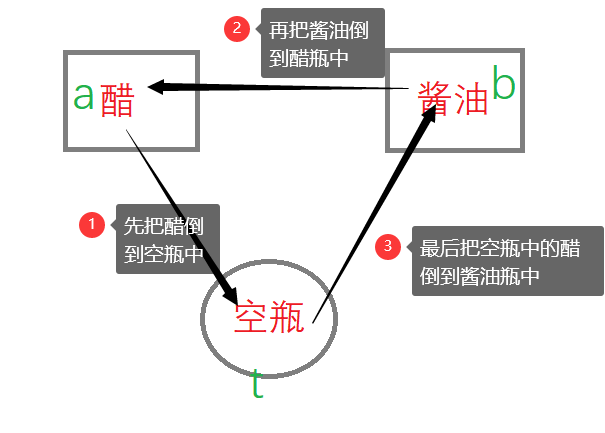
- 先把 a 赋值给 t,那么现在 t 里面存的就是 a 的值;
- 再把 b 赋值给 a,这样 a 里就是 b 的值,但 a 原本的值还在 t 里不会被覆盖;
- 最后把 t 赋值给 b,这样 a 原本的值就到了 b 中,就完成了 a 和 b 的互换。
void Swap1(int x, int y) {
int t = 0;
t = x;
x = y;
y = t;
}
void Swap2(int* px, int* py) {
int t = 0;
t = *px;
*px = *py;
*py = t;
}
int main() {
int a = 10;
int b = 20;
Swap1(a,b);
printf("Swap1:a=%d,b=%d\n", a, b);
Swap2(&a, &b);
printf("Swap2:a=%d,b=%d\n", a, b);
return 0;
}Swap1 仅仅是把 a 和 b 传值给 x 和 y,此时去修改 x 和 y 是影响不到 a 和 b 的。
Swap2 是把 a,b 的地址传给指针变量 px 和 py,这样的话,在函数内去将 px 和 py 解引用再修改,就可以指向a,b 的内容了。
简而言之,通过指针指向实参的地址使得外边的实参发生变化。
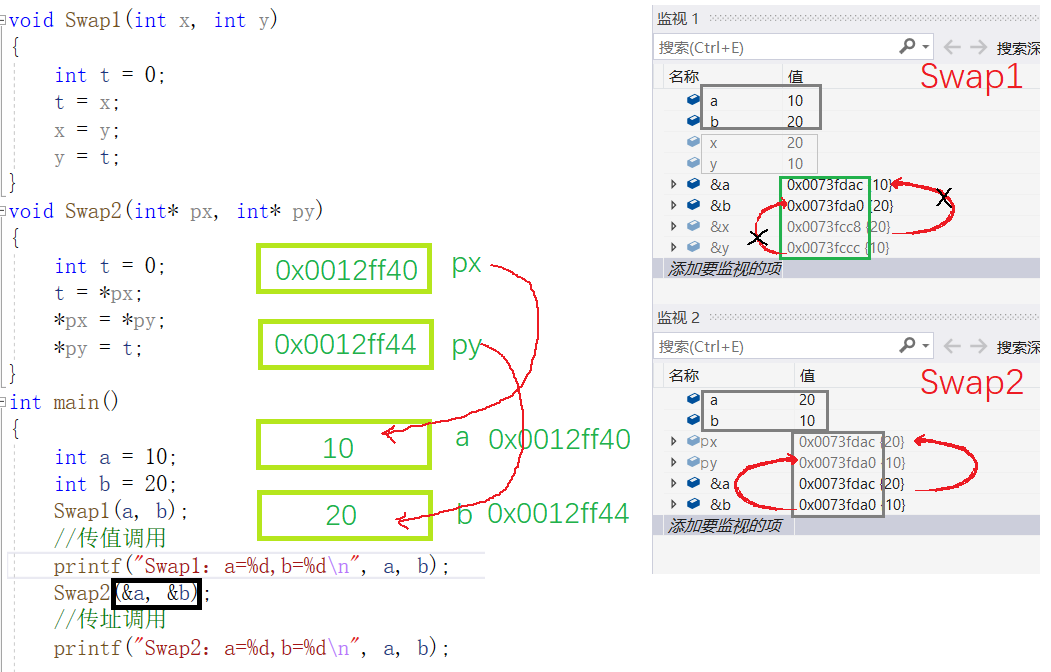
由图可知,px 和 py 内部存储的是变量 a 和 b 的地址,这样对 px 和 py 解引用就可以修改 a 和 b 的值。
由右图的监视可看出,Swap1 函数 x 和 y 确实发生了交换,但并没有影响到 a 和 b。Swap2 函数的 px、py 和 &a、&b 是一个意思。
嵌套调用
函数不可以嵌套定义,函数与函数是平等的,是并列关系,不可以在任意函数(包括主函数)中定义其他函数。但函数是可以互相调用的。
void fun1()
{
printf("hehe\n");
}
void fun2()
{
fun1();
}
int main()
{
fun2();
return 0;
}如代码所示,main函数调用fun2函数,fun2函数又调用fun1函数,最终在屏幕上打印hehe。
链式访问
链式访问(chain access),顾名思义,把一个函数的返回值作为另一个函数的参数。像是用链子把函数首尾相连拴起来。如:
int main()
{
printf("%d\n",strlen("abcde")); //把strlen的返回值作为printf的参数
return 0;
}int main()
{
char arr1[20] = "xxxxxxx";
char arr2[20] = "abcde";
//strcpy(arr1,arr2);
printf("%s\n", strcpy(arr1, arr2));//strcpy函数的返回值是目标空间首元素地址
return 0;
}如果觉得掌握了的话,可以看看这个经典例子。
printf("%d", printf("%d", printf("%d", 43)));printf 函数的返回值是打印字符的个数,如果发生错误,则返回负值。(ps:scanf 的返回值是输出字符的个数)
- 首先可以看出第三个 printf 打印了43;
- 然后第二个 printf 打印了第三个 printf 的返回值为2;
- 最后第一个 printf 打印第二个 printf 的返回值1;
所以屏幕上打印了4321。
函数声明
代码是从前往后执行的,如果在函数调用处之前并没有发现函数的定义,那么便会发出警告:函数未定义。
若想消除警告,我们便需要在前面声明一下。
void test1();
int test2() {
tes1();
}
void test1()
{}函数声明目的是告诉编译器函数的返回类型、函数名、参数这些具体信息。表示这个函数是真实存在的。
函数的声明一般出现在函数使用之前,函数的声明一般放在头文件中。
在工作的时候,一般是把函数的声明、定义和使用放在三个不同的文件内,方便所有人协作。如:
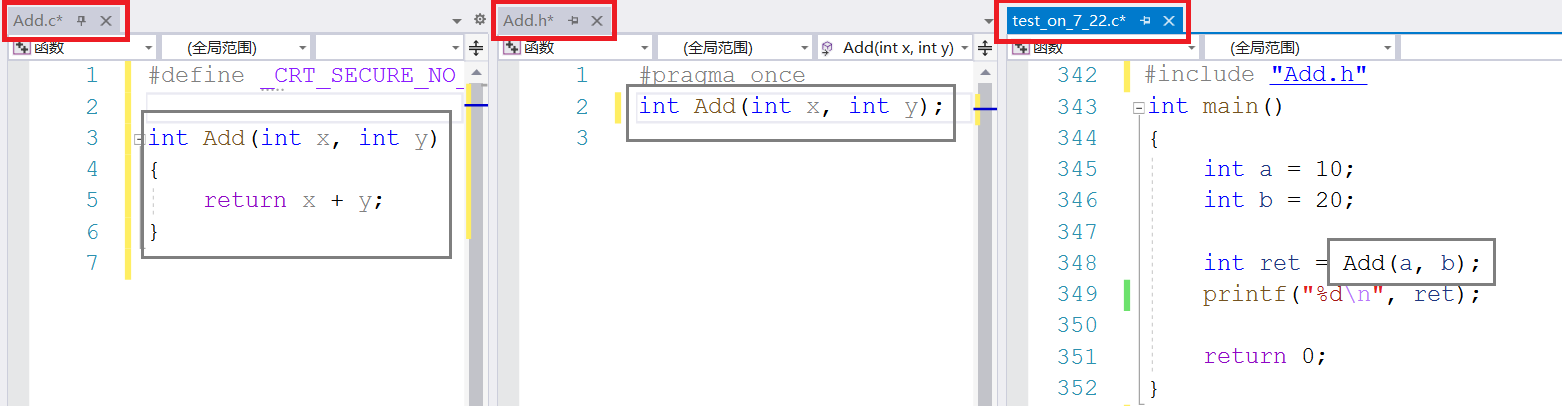
链接:两个.c的源文件编译之后,会分别生成.obj的目标文件,然后再链接起来,最后生成.exe的可执行文件。
头文件引用
#include的预编译指令是在预编译阶段将头文件内的所有内容拷贝到源文件内。头文件中的内容若被重复包含则会造成效率降低。
那么,怎么解决这件事呢?
- 头文件中包含语句
#pragma once,就可使得头文件不会被其他文件重复包含。 - 添加这样的代码,将代码包含起来。
#ifndef __ADD_H__ // if not define
#define __ADD_H__ // define
extern int Add(int x, int y); //Add函数声明
#endif // end if早期都是用第二种方法的,这两种方法是完全等价的。
函数递归
函数自身调用自身,的代码逻辑叫做递归。
- 大型复杂问题层层转化为小规模的问题
- 少量程序描述出多次运算
递归的思维方法在于:大事化小。
示例1
接收一个无符号整型值,按照顺序打印其每一位。如输入:1234,输出:1 2 3 4 .
- 创建一个函数叫print,
- 若print(1234),则剥离一位变成print(123)+4,
- 再剥离一位成print(12)+3+4,
- 再来一位就是print(1)+2+3+4,
- 最后只有一位了,
- 那就全部用
printf函数打印。如:

我们发现只要将数字1234模10就可以得到4,除10便可以得到123,如此模10除10循环往复,可以将1 2 3 4全部剥离出来。
//函数递归
void print(size_t n)
{
if (n > 9)//只有1位便不再往下进行
{
print(n / 10);
}
printf("%d ", n%10);
}具体流程可参考下面这张图。

红线部分即在返回的时候,n是本次函数n,而不是前一次调用的n。
递归递归,就是递推加回归。
现在有两个问题
if(n > 9)这个条件没有行不行?没有会怎么样?
自然是不行的,我们在上面的推导中发现,最后1<9条件不成立,就结束了递归,否则会永远递归下去,造成死循环且耗干了栈区。
- 或者是我们不论代码的正确性,将
print(n / 10)改成print(n)会怎么样?
改成
print(n)的话每次递归都是相同的值,递归也会无止境的延续下去。
这样便引出了我们递归的两个重要的必要条件:
必要条件
- 必须存在限制条件,满足条件时,递归不再继续
- 每次递归调用后必须越来越接近限制条件
栈溢出
在第一个问题中,如果我们要去试验的话,编译器会报出这样的错误:名叫Stackoverflow(栈溢出)。
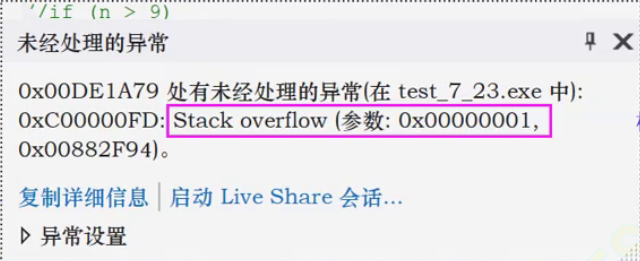
首先我们看看内存的划分:
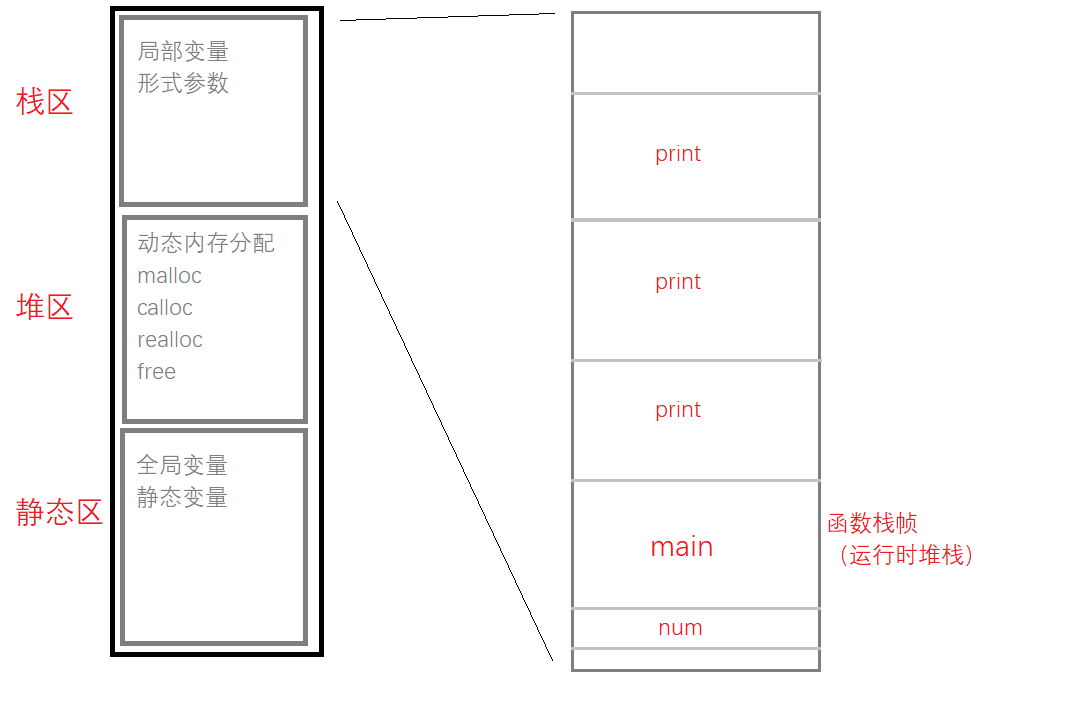
内存粗略的划分为栈区,堆区,静态区。
- 栈区主要存放:局部变量,形参(形参和局部变量差不多)
- 动态内存分配:
malloc calloc等函数开辟空间- 静态区主要存放:全局变量,static修饰的静态变量
若是把栈区放大细看的话,如图所示,有为main函数开辟的空间和print函数开辟的空间,为函数开辟的空间叫函数栈帧也可以叫运行时堆栈。
- 程序开始执行时开辟空间,程序结束时销毁空间
- 函数每调用一次就在栈上开辟一次空间,递归返回时,空间会被回收
示例2
不创建临时变量,实现Strlen函数。
//my_strlen求字符串长度
int my_strlen(char* pa)
{
if (*pa == 0)
return 0;
return 1+my_strlen(pa + 1);//直接返回长度
}具体的思考方式就是只要第一个字符不是0,那我们就在外面+1并且跳到下一个字符,直到找到‘\0’,那么我们返回0。
字符指针+1,向后跳一个字节,整型指针+1,向后跳四个字节,指针+1都是向后跳一个元素的地址,指针类型不同向后跳的字节也不同。


有这两题我们可以发现,什么时候用递归简单呢?
- 有公式有模板的时候
- 递归简单,非递归复杂的时候
当递归有明显问题的时候,就不要用递归了。
函数递归
函数递归的定义和优缺点
程序调用自身的行为就是递归。可以直接或间接的调用,本质是把复杂的问题转化为一个规模小的问题。递归一般只需少量的代码就可描绘出多次重复计算。其主要思考方式在于大事化小。
优点是为具有某些特征的编程问题提供了最简单的策略,缺点是层层调用,算法的复杂度可能过高,以致于快速耗干了计算机的内存资源,不方便阅读和维护等。
递归的使用场景及必要条件
使用场景
- 能够要求转化为新的问题,且二者解决方法相同,所处理的对象存在规律变化。
- 非递归比较麻烦,而递归很简单。
- 有模板或是公式可以直接套用,不会出现明显问题。
必要条件
- 明确存在限制条件
- 每次递归越来越逼近条件
递归的细节说明
每级递归都有自己的变量,可能名称相同,但是其值不同。
递归调用时,系统自动保留当前函数的参数变量。每次调用系统都会为函数开辟相应的空间。
每次调用都要返回值,递归执行结束后,控制权传回到上一级函数。
调用结束后,系统释放本次调用所开辟的空间,程序返回到上一次的调用点,同时获得初进该级调用的参数。
每级递归必须逐级返回,不可跳跃或间断。
函数中递归语句之前的代码,按被调函数的顺序执行,递归之后的代码,与被调函数相反的顺序执行。
递归的习题讲解
1打印整数每一位
用递归的方式,实现打印一个整数的每一位的功能。
输入输出示例
输入:1234
输出:1 2 3 4
解题思路
print(1234)$=$print(123)+4 $=$print(12)+3+4 $=$print(1)+2+3+4 $=$printf(1)+2+3+4
这便是前面使用场景中所写的,将题目要求问题转化为新的问题,且变量有规律的变化
代码逻辑
n是不是个位数,递推调用n / 10
n是个位数,回归打印n % 10
void Print(int n)
{
if (n > 9)
{
Print(n / 10);
}
printf("%d ", n%10);
}
int main()
{
int num = 0;
scanf("%d", &num);
Print(num);
return 0;
}2递归和非递归求n阶乘
用递归和非递归的方法,分别实现求n的阶乘的功能(不考虑溢出)。
输入输出示例
输入:5
输出:120
解题思路
$nn-1n-2n-3…*1$
代码逻辑
$fac(n) = n * fac(n-1) , n>0$
$fac(n) = 1 , n=0$
int fac(int n)//非递归
{
int ret = 1;
for (int i = 1; i <= n; i++)
{
ret *= i;
}
return ret;
}
int fac(int n)//递归
{
if (n > 0)
return n * fac2(n - 1);
else
return 1;
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d\n", fac(n));
return 0;
}3strlen函数模拟
输入输出示例
输入:abcdef
输出:6
解题思路
strlen(abcdef\0) 1+strlen(bcdef\0) 1+1+strlen(cdef\0) 1+1+1+strlen(def\0) 1+1+1+1+strlen(ef\0) 1+1+1+1+1+strlen(f\0) 1+1+1+1+1+1+strlen(\0)
代码逻辑
$若 ch≠0 , strlen(arr) = 1 + strlen(arr+1)$ $若ch=0 , strlen(arr) = 0$

int my_strlen(char* ch)
{
if (*ch != '\0')
{
return 1 + my_strlen(ch + 1);
}
return 0;
}
int main()
{
char ch[20] = { 0 };
scanf("%s", &ch);
printf("%d", my_strlen(ch));
return 0;
}4逆序字符串
不开辟额外空间的情况下,不使用字符串库函数,递归实现字符串反向排列,而不是倒序打印。
输入输出示例
输入:abcdef
输出:fedcba
解题思路
abcdef递推:(先把后面赋值给前面,后面用覆盖\0)
$ \Rightarrow$
f b c d e \0$\Rightarrow$
f e c \0\0$\Rightarrow$
f e d \0\0\0回归:(把前面转移出去的字符对应赋值给\0)
$ \Rightarrow$
f e d c \0\0$\Rightarrow$
f e d c b \0$\Rightarrow$
f e d c b a
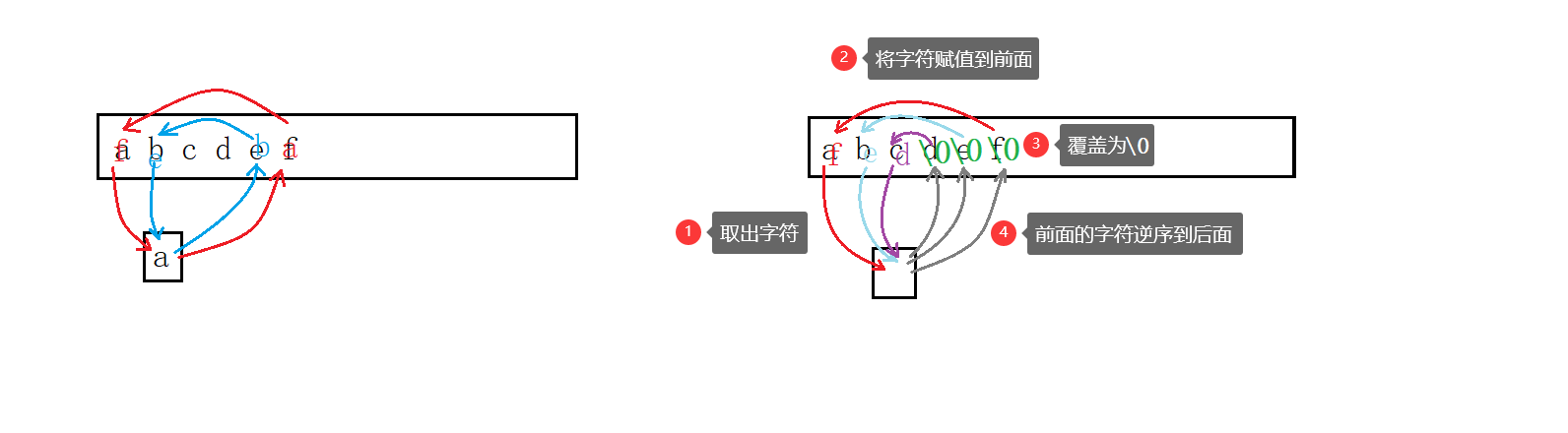
代码逻辑
reverse("abcdef\0") 交换a和f+reverse("f bcde\0\0") 交换a和f+交换b和e+reverse("fe cd\0\0\0") 交换a和f+交换b和e+交换c和d+reverse("fed \0\0\0\0")
- 交换两个字符
- 将在前的字符先放到一边存着
- 把在后的字符赋值到前面的位置
- 再把后面的位置对应覆盖为
\0- 原在前字符替换
\0
- 把事先存好的在前的字符对应替换到
\0的位置上
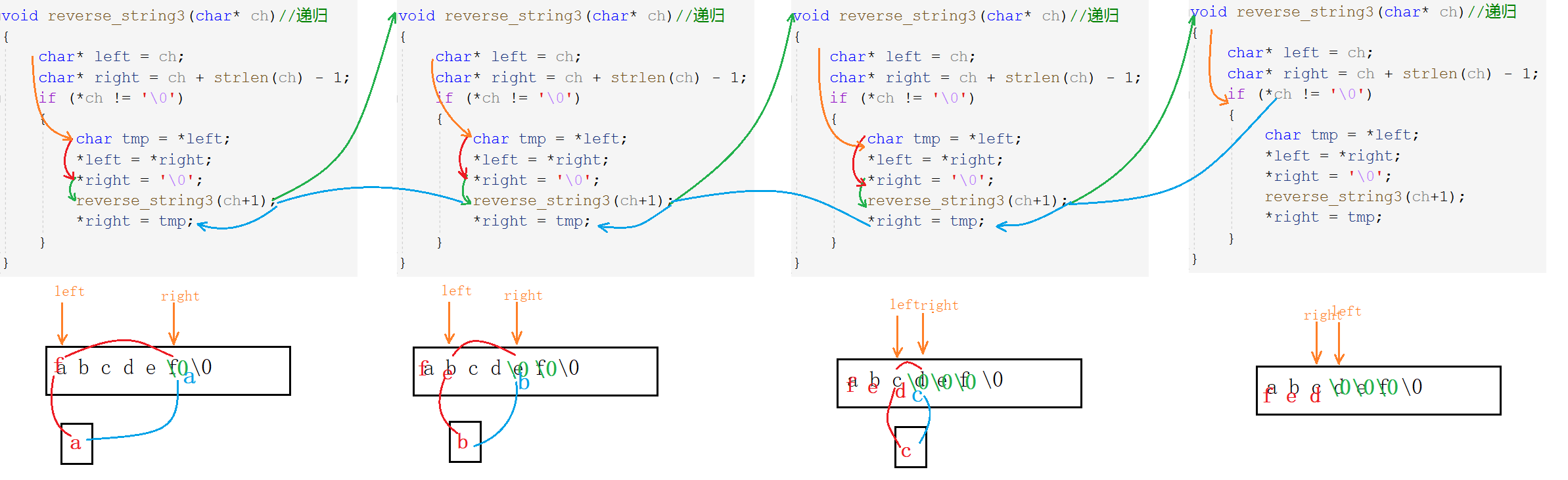
void reserve_string1(char* ch)//指针
{
char* left = ch;
char* right = ch + strlen(ch) - 1;
while (left < right)
{
char tmp = *left;//不能交换地址,只能交换内容
*left = *right;
*right = tmp;
left++;
right--;
}
}
void reserve_string2(char* ch)//数组
{
int left = 0;
int right = strlen(ch) - 1;
while (left < right)
{
char tmp = ch[right];
ch[right] = ch[left];
ch[left] = tmp;
left++;
right--;
}
}
void reverse_string3(char* ch)//递归
{
char* left = ch;
char* right = ch + strlen(ch) - 1;
if (*ch != '\0')
{
char tmp = *left;//提取
*left = *right;//赋值
*right = '\0';//赋\0
reverse_string3(ch+1);//ch+1,而不是ch++
*right = tmp;//赋值
}
}
int main()
{
char ch[20] = "abcdef";
//char* ch = "abcdef";//err - 常量字符串不可修改
reverse_string3(ch);
printf("%s\n", ch);
return 0;
}5递归实现数字各位之和
写一个递归函数DigitSum(),输入一个非负整数,返回组成它的数字之和
输入输出示例
输入:1234
输出:10
解题思路
1234
DigitSum(123)+4DigitSum(12)+3+4DigitSum(1)+2+3+41+2+3+4
1234%10=4 1234/10=123
123%10=3 123/10=12
12%10=2 12/10=1
1%10=1 1/10=0
一个数模10得到尾数,除10得到尾数前面的数字
通过不断的除10模10,就可以把每一位数字放到末尾,从而得到每一位数字
代码逻辑
若n不为个位数,先%10得到尾数,再/10
一定要有递归的出口,即当n为个位数时,函数返回n
int DigitSum(int n)
{
if (n > 9)
return DigitSum(n / 10) + n % 10;
else
return n;//递归的出口
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d\n", DigitSum(n));
return 0;
}6求n的k次幂
输入两个整数分别代表底数和次幂,递归实现n的k次幂的功能。
输入输出示例
输入:2 3
输出:8
解题思路
当
k>0时,函数返回n*power(n,k-1)当
k=0时,函数返回1,这是程序的出口,是程序递归到最后必须要计算的值
代码逻辑
$n^k = n * n^{k-1} ,k > 0$ $n^k = 1 , k = 0$
double power(int n,int k)
{
if (k > 0)
return n * power(n, k - 1);
else if (k == 0)
return 1.0;//递归的出口k=0
else
return 1.0 / power(n, -k);
}
int main()
{
int n = 0;
int k = 0;
scanf("%d%d", &n, &k);
printf("%lf\n", power(n, k));
return 0;
}7递归求斐波那契数列
递归和非递归分别实现求第n个斐波那契数
输入输出示例
输入:5
输出:5
解题思路
$1\quad 1\quad 2\quad 3\quad 5\quad 8\quad 13\quad 21\quad 34\quad 55\quad 89\quad ...$
代码逻辑
递归:
$Fib(n) = Fib(n-1) + Fib(n-2) , n>2$ $Fib(1) = Fib(2) = 1$
非递归:
上一次的b换成这一次的a
上一次的c换成这一次的b
如此循环,就可以从前往后一个一个求。

int Fib(int n)
{
if (n > 2)
return Fib(n - 1) + Fib(n - 2);
else
return 1;
}但是这个方法效率是非常低的,当数字特别大时,层层拆分下来,时间效率是$O(2^n)$。
根据公式可知,第三个斐波那契数可由前两个得到,我们利用这个规律
int Fib(int n)
{
if (n <= 2)
return 1;
int a = 1;
int b = 1;
int c = 1;//n=3时不用运算
while (n >= 3)//从头开始移动n-2次,n=3时不用
{
c = a + b;
a = b;//b赋值给a
b = c;//c赋值给b
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d",Fib(n));
return 0;
}经典问题
汉诺塔问题
汉诺塔,小时候游戏机上经常看别人玩的,自己玩到三四局就玩不下去了的那款游戏。当然如果你觉得非常简单,小时候能玩的行云流水,那你有本事到我面前说,礼貌谢谢(狗头保命)。
游戏规则
有三根柱子,分别为A、B、C ,A柱上从上到下依次排列着由小到大的圆盘,我们需要把圆盘从A柱按照同样的摆放顺序放到C柱上,期间我们可以借助B柱。
- 每次只能挪动一个且是最上面的圆盘
- 按照从上到下依次是由小到大的顺序摆放。
解题思路
假设由N个盘子,只需要考虑第$N$个盘子和其上$N-1$个盘子的整体。显然思路就是,第$N$个是要放在$C$柱上的,
- 首先将$N-1$个整体是先放在$B$柱上;
- 其次将第$N$个放在$C$柱上;
- 最后将$N-1$个整体放到$C$柱上。
即:第$N$个$A\rightarrow B$,$N-1$个整体$A\rightarrow B\rightarrow C$ 。然后再考虑$N-1$个中把第$N-1$个当作最后一个,其上$N-2$个当作整体,到最后只剩一个直接放到$C$柱上。这便是递归的整体思路。
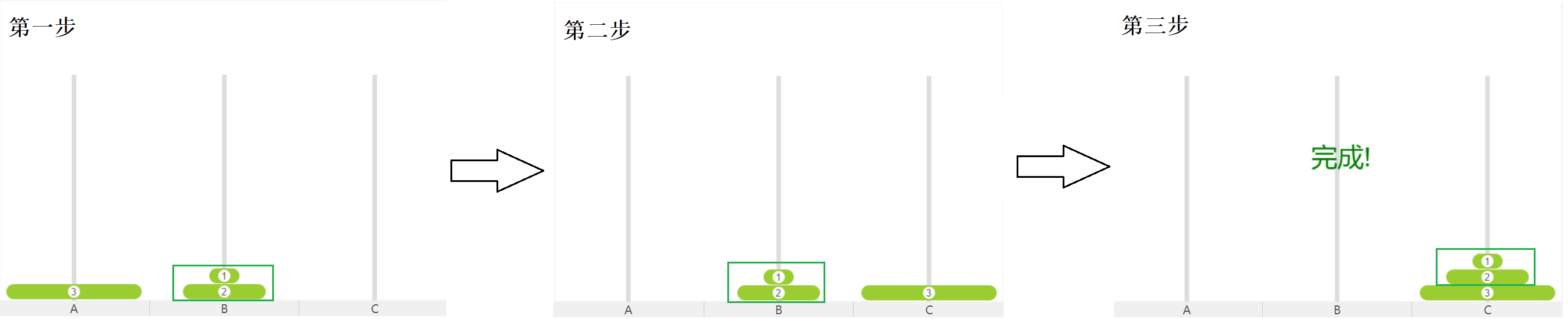
void move(int n, int x, int z)
{
printf("%d盘:%c->%c\n", n, x, z);
}
void hannoi(int n, char x, char y, char z)
{
if (n == 1)
move(n, x, z);
else
{
hannoi(n - 1, x, z, y);
move(n, x, z);
hannoi(n - 1, y, x, z);
}
}
int main()
{
int input = 0;
do
{
printf("输入盘数开始测试(0. 退出测试)\n");
scanf("%d", &input);
switch (input)
{
case 0:
break;
default:
hannoi(input, 'A', 'B', 'C');
break;
}
} while (input);
return 0;
}青蛙跳台阶
游戏规则
**初阶版本**
青蛙一次可以跳一级台阶,也可以跳两级台阶。求该青蛙跳n级台阶共有多少种跳法?
**进阶版本**
青蛙一次可以跳一级台阶,也可以跳两级台阶,……,也可以跳n级台阶,求该青蛙跳上n级台阶的跳法种数。
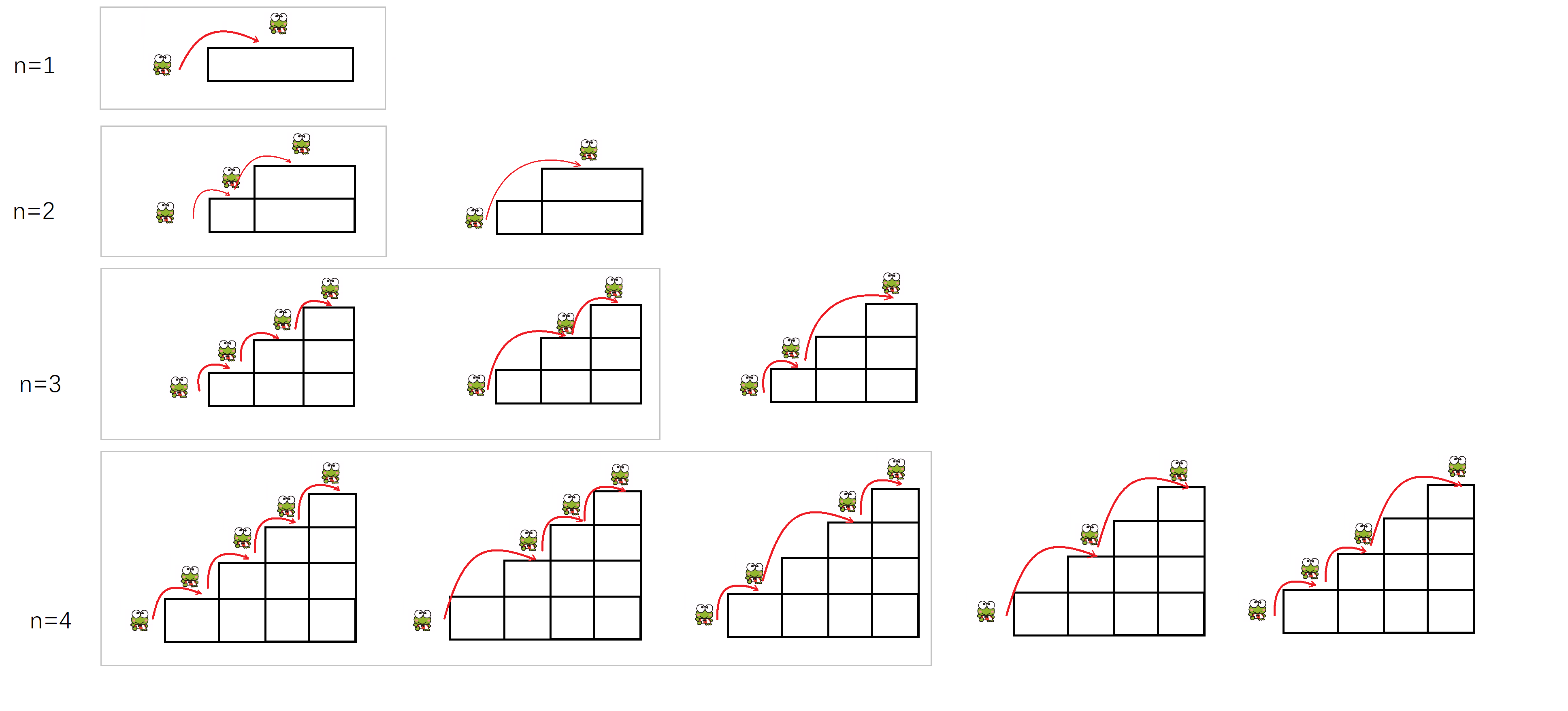
解题思路
我们反向思考,当青蛙跳到最高阶$N$阶时,他是怎么跳到第$N$阶的呢?
有两种情况,
- 从第$N-1$阶,跳到第$N$阶,最后一次跳一阶。
- 从第$N-2$阶,跳到第$N$阶,最后一次跳两阶。
图中用灰框框出的部分,是最后一次跳一阶的,其余的是最后一次跳两阶的。
很显然,除了这两种情况,别无他法。所以计算青蛙
跳到$N$阶的方法数 $=$ 跳$N-1$阶的方法数 $+$ 跳$N-2$ 阶的方法数。
同样,图中用灰框框出的部分,也代表的是跳$N-1$阶的方法数,其余的是跳$N-2$ 阶的方法数。
这其实就是斐波那契数列。
int fib(int n)
{
if (n > 1)
return fib(n - 1) + fib(n - 2);
else
return 1;
}