二叉搜索树
普通二叉树的意义不大,只有加上一些性质才能发挥其作用。比如堆和二叉搜索树。
1. 二叉搜索树的概念
二叉搜索树又称二叉排序树,它可以是一颗空树,或者是一个满足如下性质的二叉树:
- 如果左子树不为空,左子树上所有节点的值都小于根节点;
- 如果右子树不为空,右子树上所有节点的值都大于根节点;
且它的左右子树,也满足上述性质。
template<class K>
struct bstree_node
{
bstree_node<K>(K key)
: _left(nullptr), _right(nullptr), _key(key)
{}
bstree_node<K>* _left;
bstree_node<K>* _right;
K _key;
};
template<class K>
class bstree
{
public:
typedef bstree_node<K> node;
private:
node* _root = nullptr;
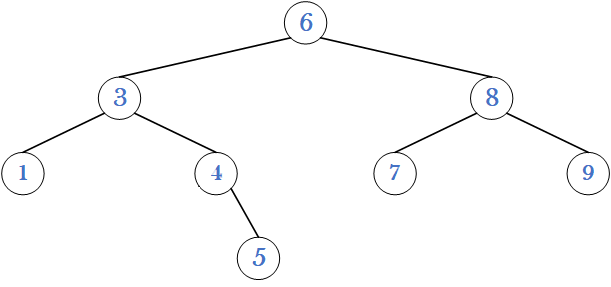
};二叉搜索树最大的问题是会退化,比如顺序插入时就会退化成一个链表。
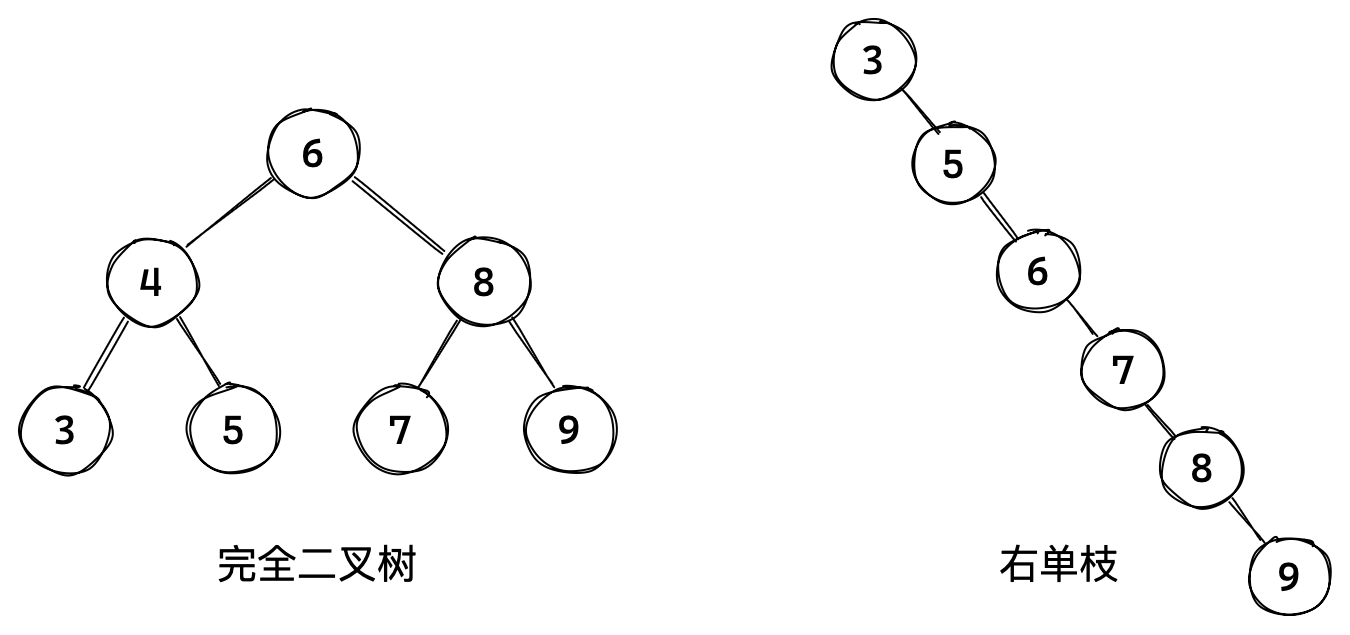
搜索二叉树的效率体现在搜索上,最坏情况搜索高度次。所以树的高度越低,性能越好。所以一般不会使用单纯的搜索二叉树,而是使用升级版的AVL树和红黑树。
2. 二叉搜索树的接口
2.1 查找
若根节点不为空:
- 如果节点值等于 $key$,返回 $true$,
- 如果节点值小于 $key$,到其右子树中查找,
- 如果节点值大于 $key$,到其左子树中查找,
走到空树还没找到,则返回 $false$。
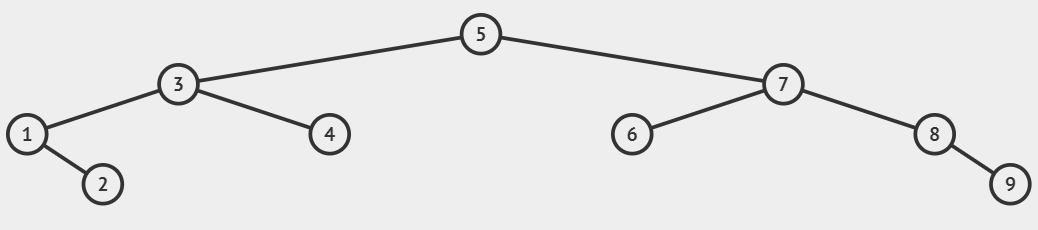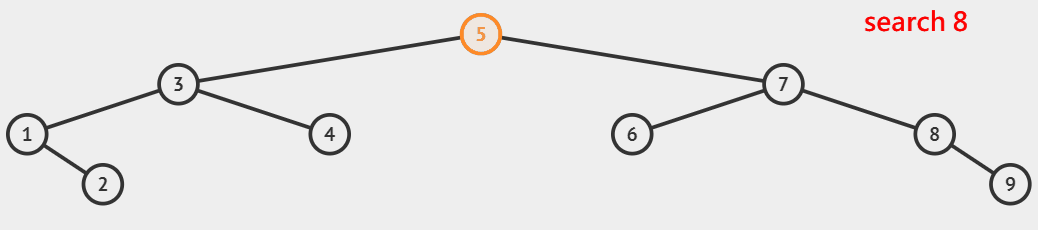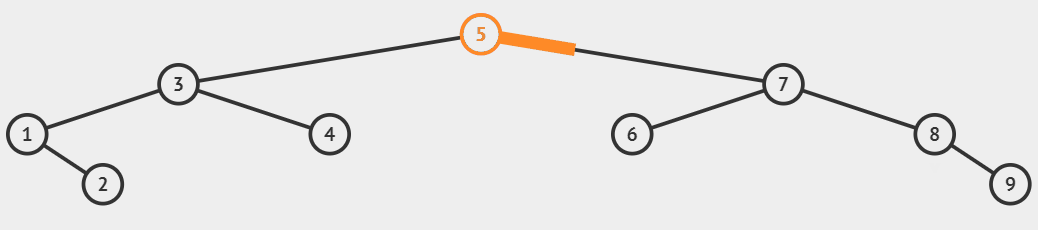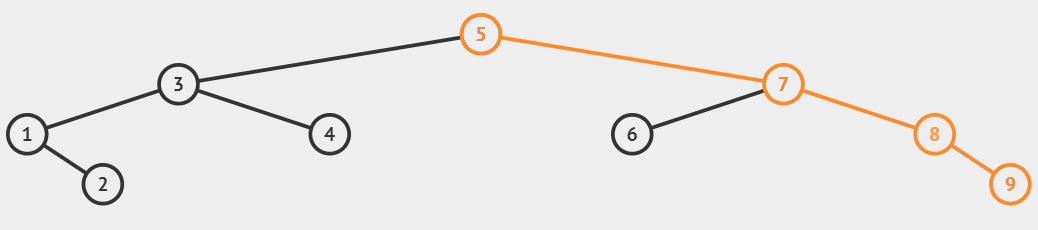
非递归查找
bool find(const K& key)
{
node* cur = _root;
while (cur)
{
if (key < cur->_key)
cur = cur->_left;
else if (key > cur->_key)
cur = cur->_right;
else
return true;
}
return false;
}二叉搜索树的查找非常的迅速,在二叉树相对平衡的情况下,时间复杂度高度次 $O(logN)$。最差是线性状态,为 $O(N)$。
递归查找
bool find_r(const K& key)
{
return _find_r(_root, key);
}
bool _find_r(node* root, const K& key)
{
if (root == nullptr)
return false;
if (key < root->_key)
return _find_r(root->_left, key);
else if (key > root->_key)
return _find_r(root->_right, key);
else
return true;
}2.2 中序遍历
二叉搜索树的中序遍历结果,就是树中元素排成升序的结果。
void inorder()
{
_inorder(_root);
std::cout << std::endl;
}
void _inorder(node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
std::cout << root->_key << " ";
_inorder(root->_right);
}一般成员函数在类外调用时,无法直接传入成员变量作参数。故可以将主体逻辑包装成子函数,再由成员函数去调用即可。
void TestBSTree()
{
BSTree<int> t;
int a[] = { 7,1,3,6,4,8,7,9,3,2,5 }; //排序数组
for (auto e : a) {
t.Insert(e); //插入二叉搜索树
}
t.Inorder(); //中序遍历
}如上代码,相当于利用二叉搜索树排序数组,而二叉搜索树结构天然具有排序加去重的功能。
2.3 插入
二叉搜索树的插入也很简单,共分两种情况:
- 树为空,则直接插入,
- 树不为空,则按性质查找到插入位置,再插入新节点。
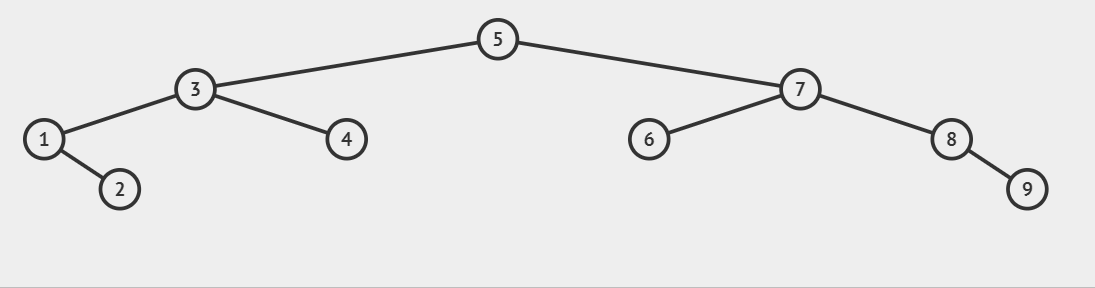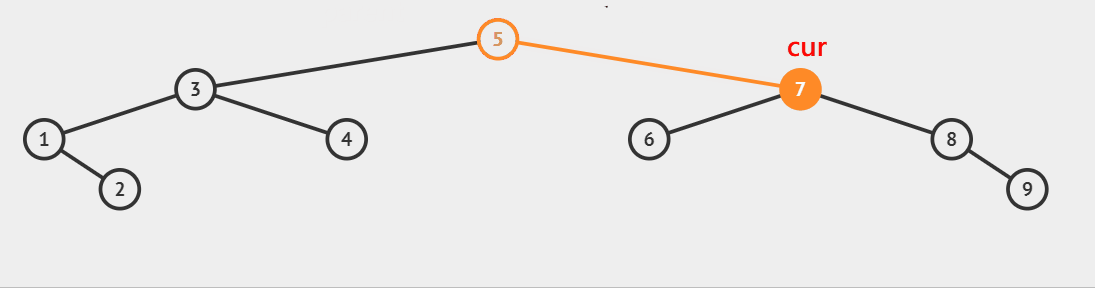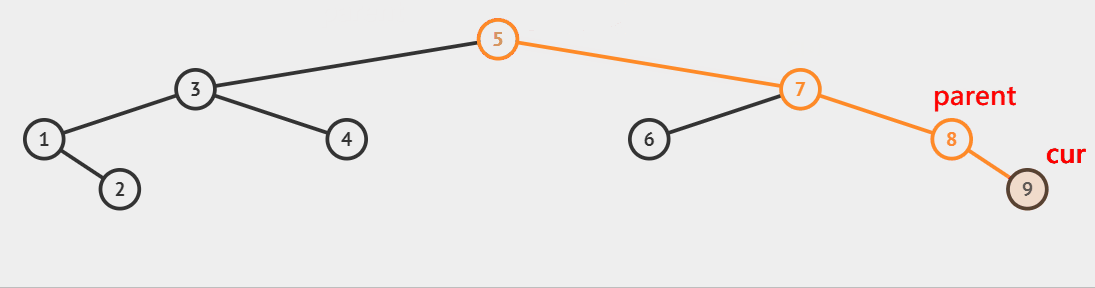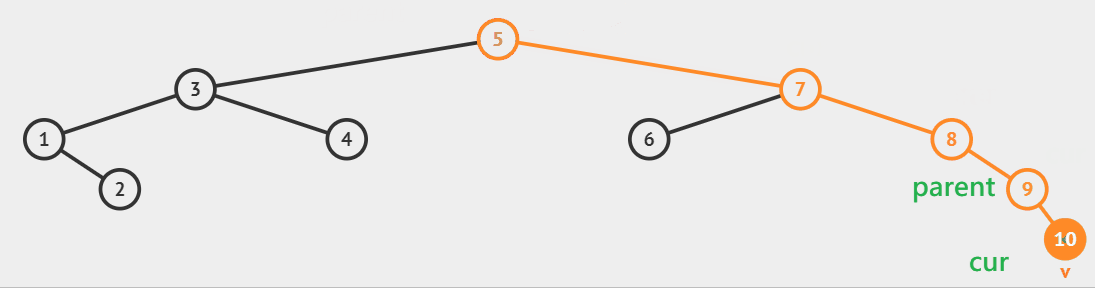
cur指针进行比较并向下移动的同时,父指针parent始终指向cur的父节点。当cur走到空的时候,就创建新节点并链接到父节点的指针上。
- 插入的值比当前节点的值小,则插入到左子树中,
- 反之,比当前节点的值大,则插入到右子树中。
非递归插入
bool insert(const K& key)
{
if (_root == nullptr)
{
_root = new node(key);
return true;
}
node* cur = _root;
node* parent = nullptr;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
return false;
}
if (key < parent->_key)
parent->_left = new node(key);
else
parent->_right = new node(key);
return true;
}可见,二叉搜索树的每次插入都是把节点放在叶节点的位置上。
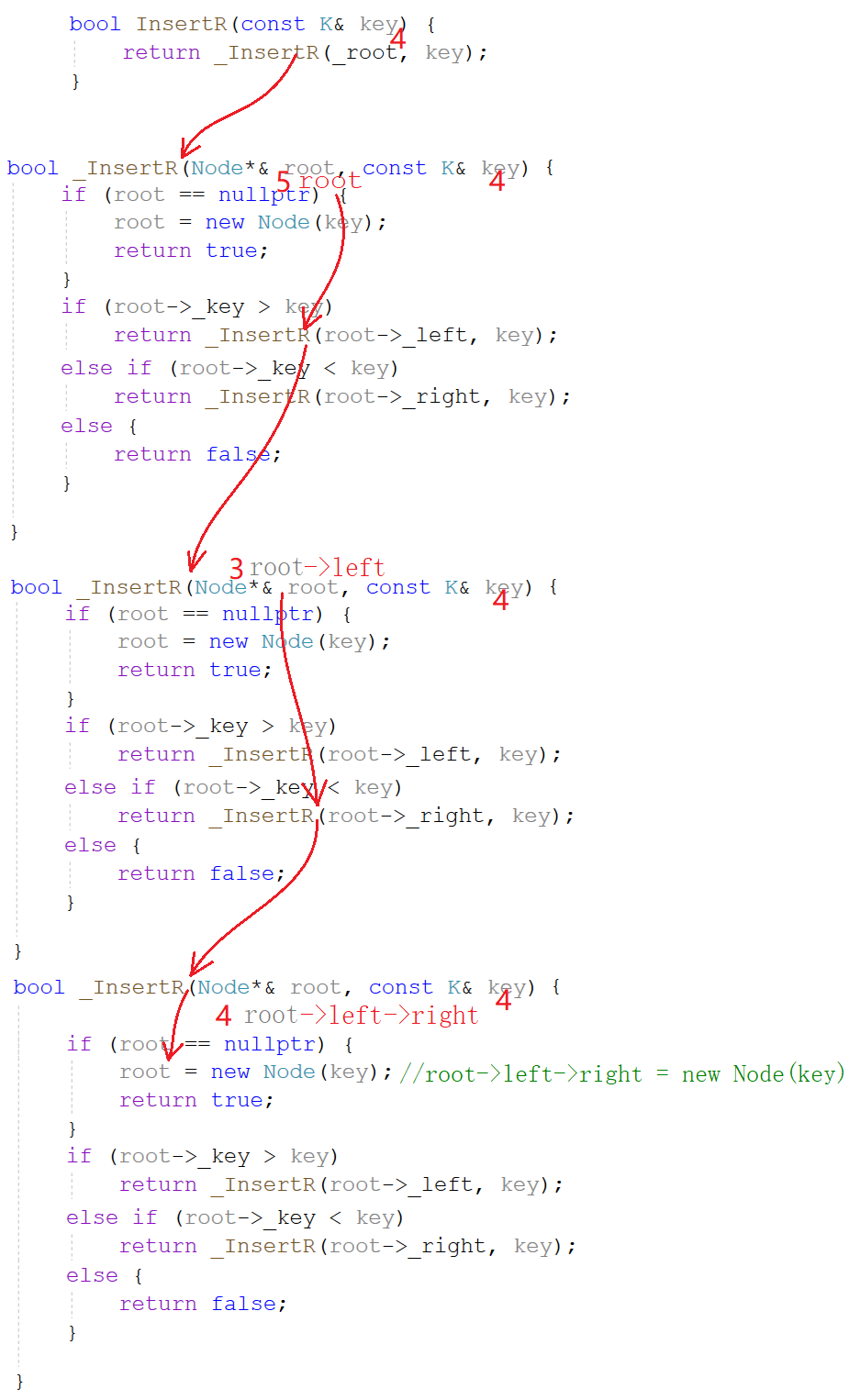
递归插入
bool insert_r(const K& key)
{
return _insert_r(_root, key);
}
bool _insert_r(node*& root, const K& key)
{
if (root == nullptr)
{
root = new node(key);
return true;
}
if (key < root->_key)
return _insert_r(root->_left, key);
else if (key > root->_key)
return _insert_r(root->_right, key);
else
return false;
}参数类型是节点指针的引用,使得root不仅是节点指针,还是其父节点的左或右孩子指针,修改root也就修改了父节点的左右孩子。
2.4 删除
二叉搜索树的难点在于删除,因为节删除节点需要维护剩余节点的链接关系。
删除叶节点很容易,释放节点并置空父节点的指针即可。删除非叶结点,可以将子树中满足条件的节点替换上来。
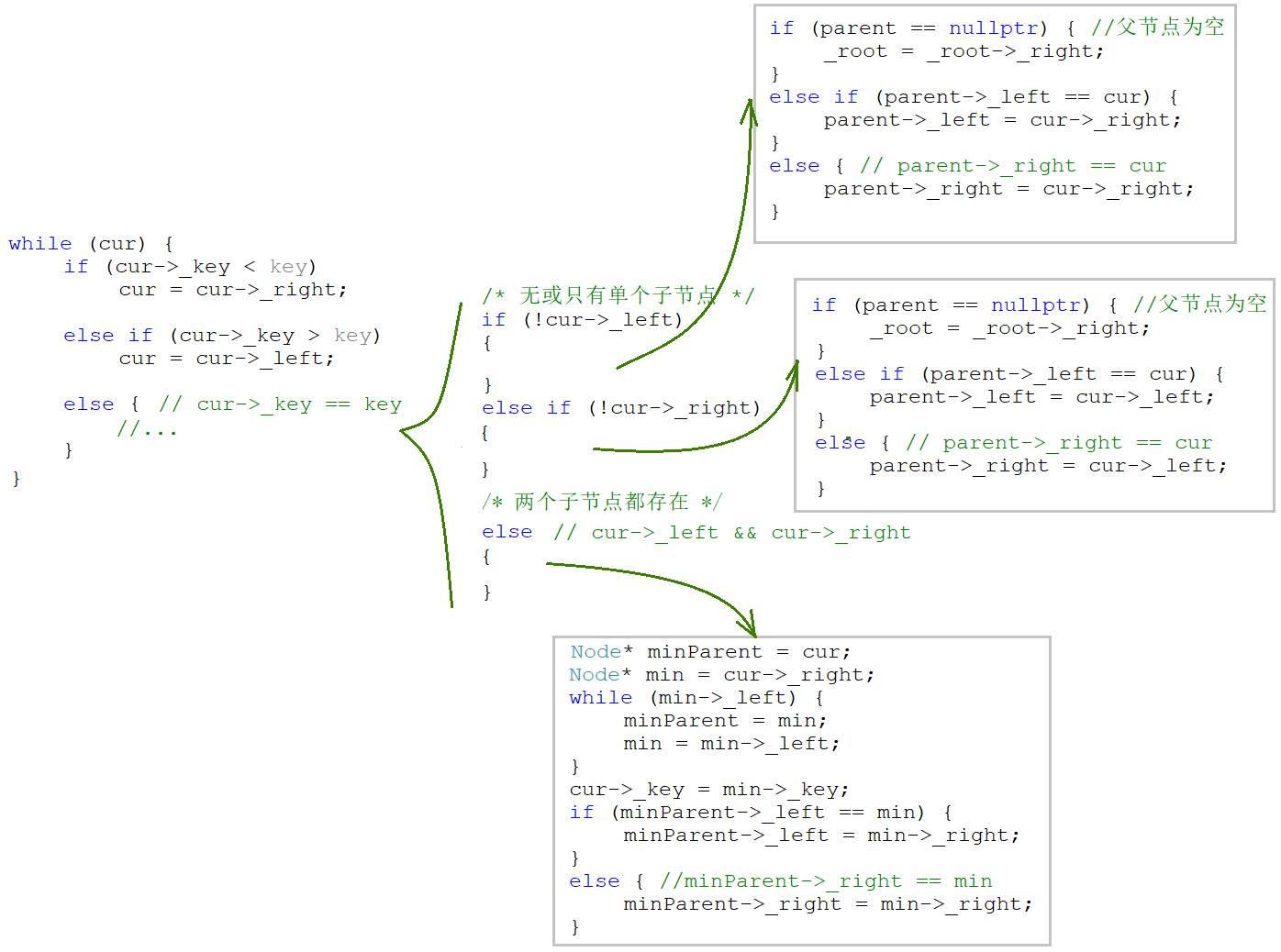
如果节点不存在先返回 $false$,如果存在,则分以下几种情况:
| 直接删除 | 解释 |
|---|---|
| 删除的节点有单个子节点 | 左为空就让父节点指向右子树,右为空就让父节点指向左子树 |
| 删除的节点无子节点 | 归类到上一类处理 |
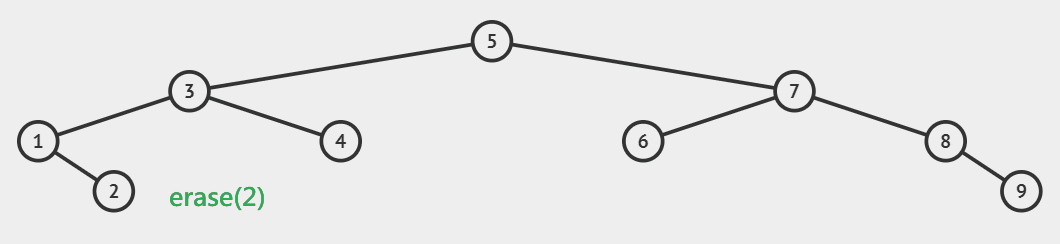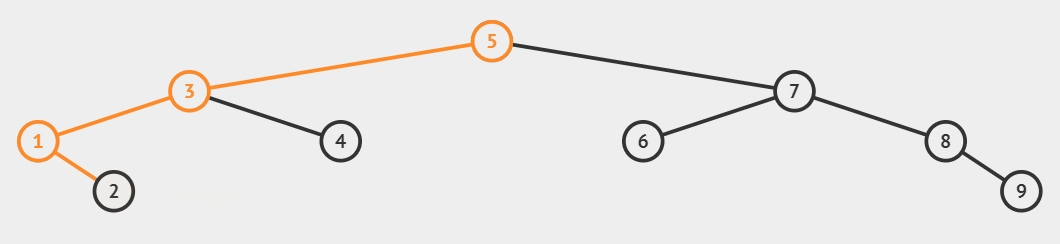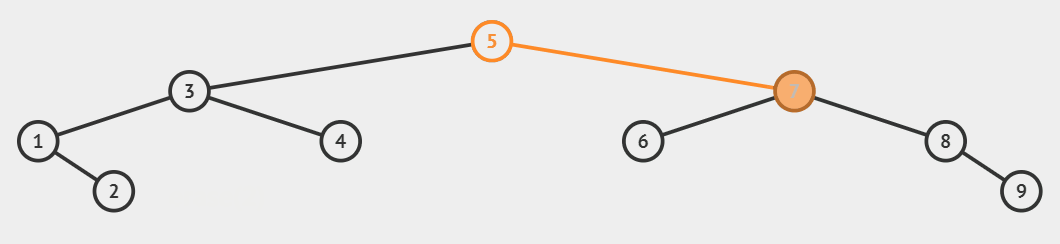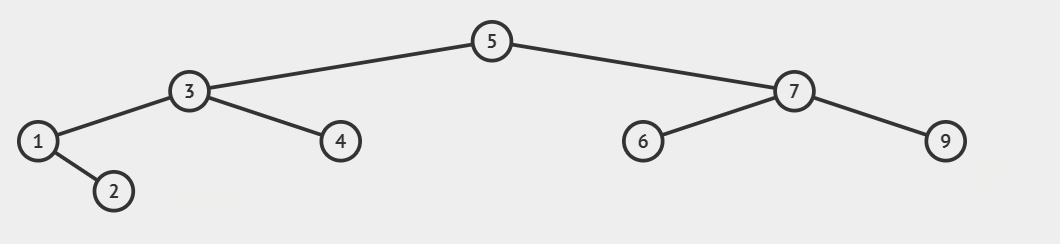
| 替换删除 | 解释 |
|---|---|
| 删除的节点左右子节点都有 | 用左树的最大节点,或右树的最小节点,替换被删节点。 |
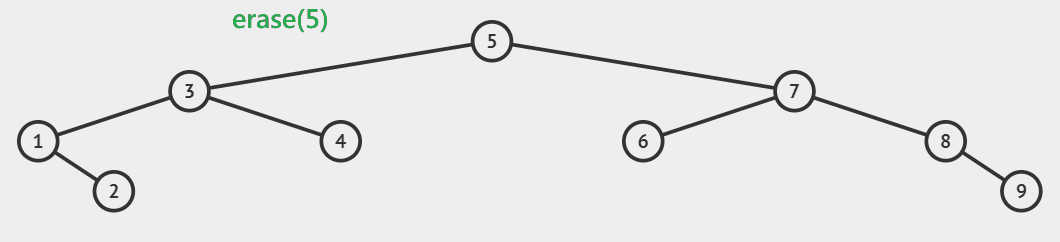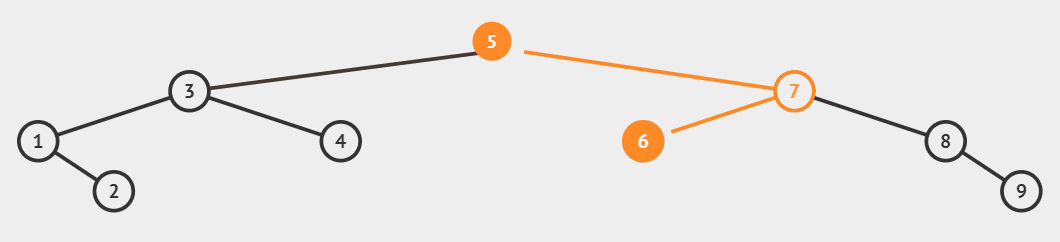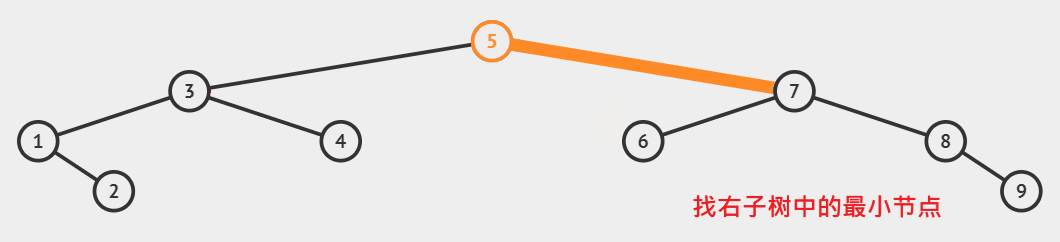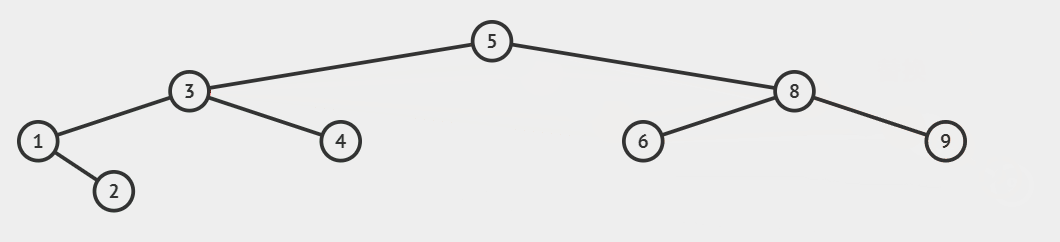
- 先将左树最大节点的左孩子托,或是右树最小节点的右孩子托付给父节点。
- 再将左树最大节点覆盖待删除的节点。
非递归删除
bool erase(const K& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
if (!cur->_left)
{
if (parent == nullptr)
_root = _root->_right;
else if (cur == parent->_left)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
delete cur;
}
else if (!cur->_right)
{
if (parent == nullptr)
_root = _root->_left;
else if (cur == parent->_left)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
delete cur;
}
else
{
#ifdef 方式1
node* min = cur->_right;
while (min->_left)
min = min->_left;
K minkey = min->_key;
erase(min->_key);
cur->_key = minkey;
#endif
#ifdef 方式2
node* min_parent = cur;
node* min = cur->_right;
while (min->_left)
{
min_parent = min;
min = min->_left;
}
cur->_key = min->_key;
if (min == min_parent->_left)
min_parent->_left = min->_right;
else
min_parent->_right = min->_right;
delete min;
#endif
}
return true;
}
}
return false;
}
递归删除
bool erase_r(const K& key)
{
return _erase_r(_root, key);
}
bool _erase_r(node*& root, const K& key)
{
if (root == nullptr)
return false;
if (key < root->_key)
return _erase_r(root->_left, key);
else if (key > root->_key)
return _erase_r(root->_right, key);
else
{
node* del = root;
if (!root->_left)
root = root->_right;
else if (!root->_right)
root = root->_left;
else
{
node* min = root->_right;
while(min->_left)
min = min->_left;
// min = min->_right; // ERR
root->_key = min->_key;
// return _erase_r(min, min->_key); // ERR
return _erase_r(root->_right, min->_key);
}
delete del;
return true;
}
}
3. 二叉搜索树的应用
搜索树有两种应用,key搜索模型和key/value搜索模型。此外,二叉搜索树插入重复值会失败,所以自带去重功能。
key搜索模型
key搜索模型查找返回真假,只能用来判断数据是否存在。应用场景如存储车牌号判断是否放行等。
kv搜索模型
通过key查找对应value,两个值是强相关的映射关系。 应用场景如中英互译,身份绑定等。
template<class K, class V>
struct bstree_node
{
bstree_node<K, V>* _left;
bstree_node<K, V>* _right;
K _key;
V _val;
bstree_node<K, V>(const K& key, const V& val)
: _key(key), _val(val), _left(nullptr), _right(nullptr)
{}
};
template<class K, class V>
class bstree
{
typedef bstree_node<K, V> node;
public:
bool insert(const K& key, const V& val)
{
if (_root == nullptr)
{
_root = new node(key, val);
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
return false;
}
if (key < parent->_key)
parent->_left = new node(key, val);
else if (key > parent->_key)
parent->_right = new node(key, val);
return true;
}
node* find(const K& key)
{
node* cur = _root;
while (cur)
{
if (key < cur->_key)
cur = cur->_left;
else if (key > cur->_key)
cur = cur->_right;
else
return cur;
}
return nullptr;
}
bool erase(const K& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
if (!cur->_left)
{
if (!parent)
_root = _root->_right;
else if (cur == parent->_left)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
delete cur;
}
else if (!cur->_right)
{
if (!parent)
_root = _root->_left;
else if (cur == parent->_left)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
delete cur;
}
else
{
node* min_parent = cur;
node* min = cur->_right;
while (min->_left)
{
min_parent = min;
min = min->_left;
}
cur->_key = min->_key;
cur->_val = min->_val;
if (min == min_parent->_left)
min_parent->_left = min->_right;
else
min_parent->_right = min->_right;
delete min;
}
return true;
}
}
return false;
}
void inorder()
{
_inorder(_root);
cout << endl;
}
void _inorder(node* root)
{
if (!root)
return;
_inorder(root->_left);
cout << root->_key << "-" << root->_val << endl;
_inorder(root->_right);
}
private:
node* _root = nullptr;
}
5. oj题
| OJ链接 | 题解链接 |
|---|---|
| 606. 根据二叉树创建字符串 | 题解 |
| 102. 二叉树的分层遍历 | 题解 |
| 107. 二叉树的层序遍历 II | 题解 |
| 236. 二叉树的最近公共祖先 | 题解 |
| 剑指 Offer 36. 二叉搜索树与双向链表 | 题解 |
| 105. 从前序与中序遍历序列构造二叉树 | 题解 |
| 106. 从中序与后序遍历序列构造二叉树 | 题解 |
| 144. 二叉树的前序遍历 | 题解 |
| 94. 二叉树的中序遍历 | 题解 |
| 145. 二叉树的后序遍历 | 题解 |